Basic Algorithms
The Very Basics
- rolling hash instead of rolling window of string as it is faster
Backtracking
- Similar to DFS, but with rejection criteria to continue in a given path or not.
- Examples: Finding a subset of a set of positive integers S that sums up to a particular number T, where S = {10, 7, 5, 18, 12, 20, 8} and T = 23.
Dynamic programming
Two pointers
- In Linked Lists pointers to different nodes, overcomes the restriction of traversing only in one direction.
- Fast runner, slow-runner.
- Start pointer and End pointer going towards each other.
- Examples: remove duplicates from sorted array, reverse string, reverse nodes in a list, detect cycle.
Arithmetic operations
- Arithmetic operations aren’t always constant time. Multiplying big numbers is much slower than multiplying small numbers.
- Operations are not all the same speed. Integer modulus is very fast, addition and multiplication are fast, while division is (relatively) slow.
- Some number theory: You can multiply the residues of numbers, instead of the numbers themselves. But you cannot divide by residues, or divide the residues unless you have certain guarantees about divisibility.
(a + b + c ) % mis the same as(a % m + b % m + c % m) % m(a * b) % mis the same as((a % m) * (b % m)) % m- get each digit from a number
while(number > 0) {number & 10; number /= 10;}
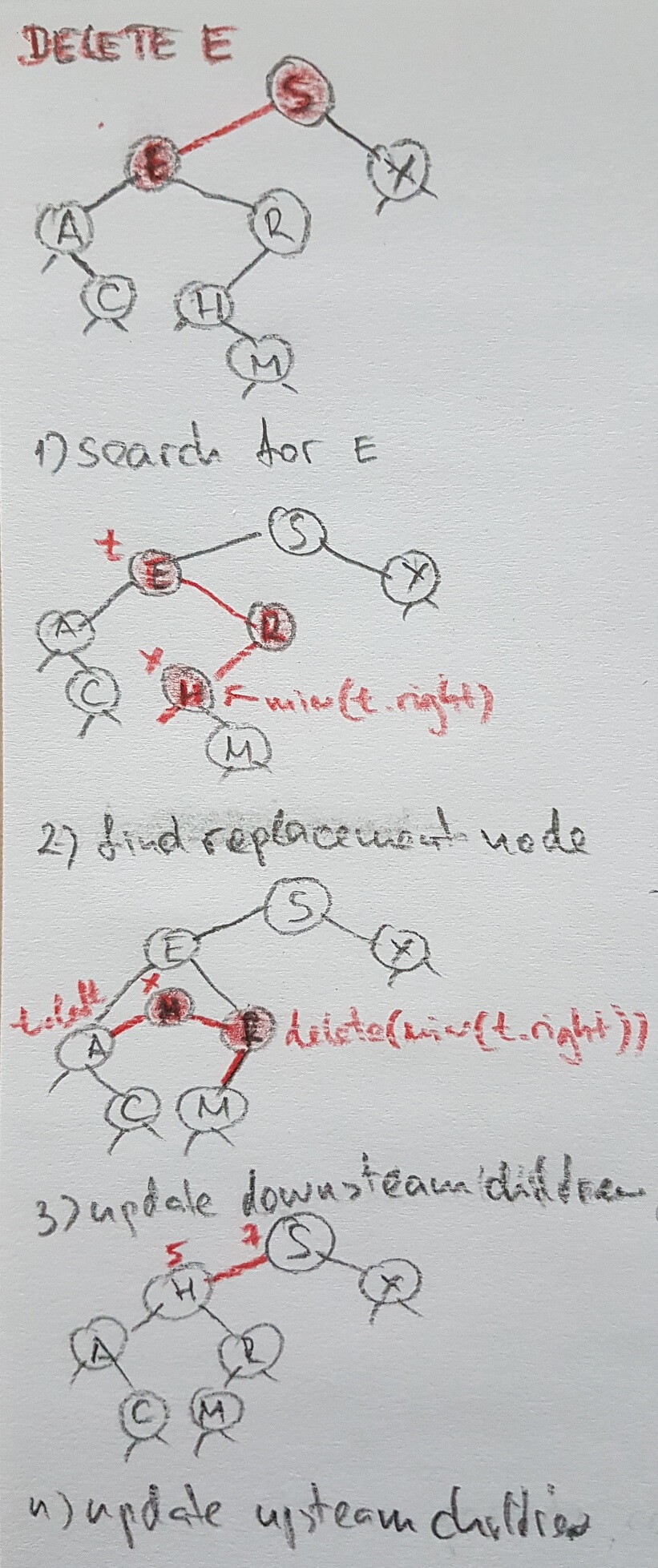
Tree remove
Graphs
- max edges = $n(n-1)/2$ , where $n$ is vertices
- a lot of edges => dense, else sparse
- Depending on the density(sparsity) think whether it will be more efficient to iterate through the edges or vertices.
- common representations:
- adjacency-list (list of lists):
list = [[1,2],[0,2,3],[0,1],[1]], where the list index is the vertex, and the inner list contains the connected vertices. An edge[i,j]is represented by havingjinlist[i]. - adjacency-matrix:
matrix = [[0,1,1,0], [1,0,1,1], [1,1,0,0], [0,1,0,0]], pay attention to the representation of “no edges”, especially in weighted graph.
- adjacency-list (list of lists):
- Examples:
- shortest path => BFS
- shortest path in weighted => Dijkstra (BFS with minPQ(compare to startNode) // add non-tree node closest to the startNode). Similar to Prim. time: E log V
- shortest path in negative weights => Bellman-Ford // time: VE.
- V1: loop nodes-1 times over edges and relax their vertices from start node; loop once again (nodes-th loop) and in case of relaxation => negative cycle => no shortest path
// relax(u,v) means find shorter path from start to v, considering u->v relax(u,v){ if(dist(start, v) > dist(start, u) + weight(u, v)){ dist(start, v) = dist(start, u) + weight(u, v); // set the u->v edge as the valid one predecessor(v) = u } } - cycle detection => DFS (+ nodes on current path, if track is kept)
- MST node-by-node => Prim (BFS with minPQ(compare to closest node on tree) // add non-tree node closest to the tree). Similar to Dijkstra // space: V time: E log V
- Topological sort => DFS (postOrder.reverse + cycle detection)